J 的艺术,R 的艺术
今天在微博上看到日本航空(JAL)的视频广告(Youtube 和腾讯视频),这个广告叫做《The Art of J》(J 的艺术),共分三篇,分别是《Precision》、《Privacy》和《CONNECTIONS》(精度、隐私和连接)。广告视频拍摄得很美,比如《Precision》中厨师凭着高超的技艺使每一个手工做出的寿司重量都是 27 克,打出的广告语是“Precision is in our culture.”(精度在我们的文化中),五次获得世界上最准时航班的殊荣,用手工难于控制的寿司重量与航班的精准形成对应的阅读关系。接着的《Privacy》是来讲座椅空间和乘坐环境的私密性好,没有什么东西能来打扰你,一位折纸艺术家在他的商务舱内作出了一件复杂又漂亮的折纸作品。通过 JAL 的网站可以看到这是他们商务舱的座位,这一套的座位设计以直线型为主,在转角等地方使用了很多三角元素,看上去整个空间都是平整和有效率,不受打扰。

但是在看《Privacy》这个视频时,全程都在受打扰,而打扰来自于旋转桌,这个带圆角的旋转桌设计与整体舱位设计看上去有点格格不入,大圆角与小圆角的直线折角设计,更怪异的是这个桌子的四个圆角还是不一样的大小,绕着顺时针方向一级级增大。

有意思的是,《Privacy》这支广告中的道具摆设却很细致,看上图这个具有颜色渐变的纸片的排列,右上和右下两处角落的纸片似乎在印证 1 和 2 两处的圆角大小不同,虽然左下违背了这一规律,但是可以看出上图的四个圆角依次在增大,按照 JAL 的网站对这个旋转桌子的示意,可以判断这几处的圆角设计并不是因为旋转这个功能需要来确定的,或许通过圆角的大小在示意旋转的方向,如果是这样就太过于隐晦了。
比圆角大小更“干扰”人的是圆角处理,设计师使用了简单的圆角工具,圆弧与两头直线的过渡方式只是 G1 切线连续,看右上角的大圆角处尤其明显,两段直线,中间一段 1/4 的圆弧形成的圆角。
如今人们经过 Apple 产品的美学特征熏陶,尤其是 2013 年 iOS 7 发布时,将界面的圆角四边形图片也改成了曲率连续的圆角四边形后,不只是设计师,大众对这些细节的处理也敏感和直接了,或许以前只是觉得不太顺畅,现在就会立刻发觉。在平面上讨论圆角的形态,各种连续的表现,[ i D 公 社 ] 在 2009 年就经过一次讨论。
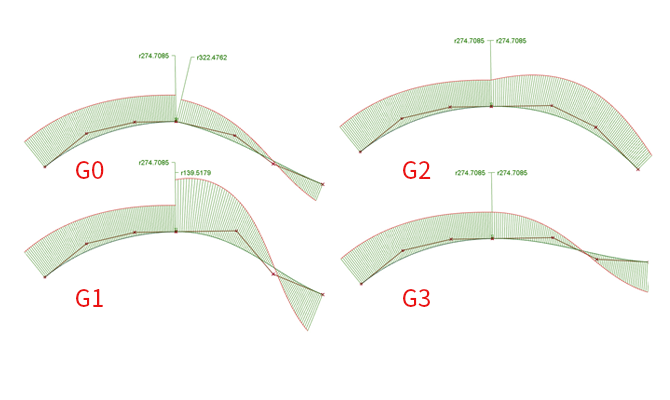
G0 还是 G1 连续指的是两条曲线形成连接的数学关系(直线是曲线的一种),曲线具有曲率(按定义说就是曲线上某个点的切线方向角对弧长的转动率),大小即曲率半径的倒数,所以通常我们说一条曲线越平缓,越接近直线也就是它越“不曲”,就是曲率越小,曲率越大曲线就越弯曲。连续就是调查连接处的曲率关系。
如上图所示(图形来自与 Alias 帮助页面),有 G0、G1、G2 和 G3 四种连续,G3 以上的连续可以按 G3 的描述向上理解,但是除了特殊需求,通常很少用到 G3 以上的连续。上图绿色的如梳子一样的线,表示着此处曲率的大小(越长曲率越大),称作曲率梳状线,曲率梳状线的外轮廓形成曲线也是连续的。G0(位置连续)指的是两条曲线相连接,但是两条曲线仅仅是相连接,在连接点位置的切线方向不一致,所以梳状线在此处形成了一个角度。G1(切线连续)指的是两条曲线不仅仅是相连接,在连接点位置的切线方向一致,但是曲率半径的大小不相等,所以梳状线在此处虽然共线但各有长短。G2(曲率连续)指的是两条曲线不仅仅是相连接,在连接点位置的切线方向一致,而且曲率半径的大小也相等,所以梳状线在此处不仅共线而且长短相同。G3(曲率连续)指的是两条曲线不仅仅是相连接,在连接点位置的切线方向一致,而且曲率半径的大小也相等,进一步在此处的曲率变化率也是相同,所以梳状线在此处不仅共线而且长短相同,而且梳状线的外轮廓线在连接点位置是切线连续的。更高阶的连续形式就是依次往下推进。
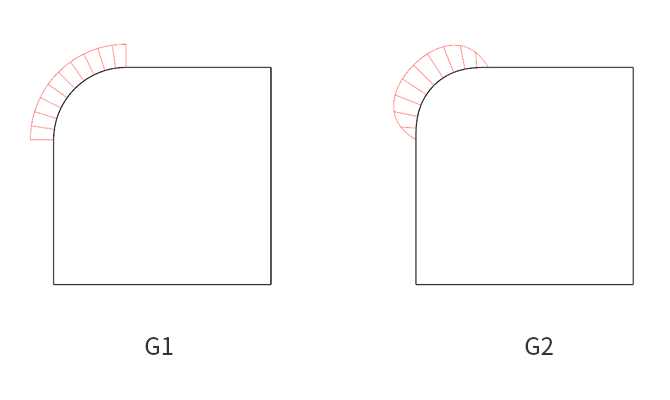
在直角上形成的圆角如上图所示,仅仅以 G1 和 G2 为例子,直线的曲率为 0,它的曲率变化率也为 0,所以在与直线相连时,G3 及更高的连续没有意义。G1 就是使用 1/4 的圆弧来形成两条直线的连接的,圆弧的曲率在曲线的每一处都是相等的,所以与直线相连,就形成了从 0 到某一个曲率的跳动,在视觉效果上就是曲线的不连续感,在曲率发生变动的一段。而 G2 保证了曲率从 0 逐渐增大的过程,所以在视觉效果上它是连续光滑的。而从直线到曲线不同的过渡形态,也会带来不同的结果。
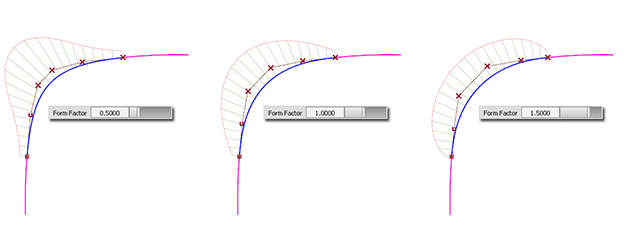
上图来自这,显示了同一连续条件下,即 G2 曲率连续情况下,不同的过渡形态,可以从梳妆线的形状来对比,即曲率变化的加速度的不同。左图为先缓和再急剧在缓和,右图为先急剧再缓和(接近匀速)在急剧,中间的为介于两者之间,左图容易在中间形成曲率的最大值,而右图中端更接近圆形。
在用 G2 连续的曲线来制作圆角时,一般需参照上图右的梳状线形态,因为我们需要用一条曲率连续变化的曲线来模拟曲率恒定的圆,G0 连续的圆角即 1/4 圆弧虽然在头尾处的曲率突变给人带来不顺畅的视觉体验,但是它的圆度是确定的,我们用 G2 连续的曲线来制作,除了需照顾到头尾过度的顺畅,还要照顾到它的中间段与圆足够接近,也就是要求保证它的圆度,让它的曲率看上去尽可能相同,那么在圆角上,我们识别到“曲”的地方就是中间段,所以它的曲率变化梳状线应该如右图所示。
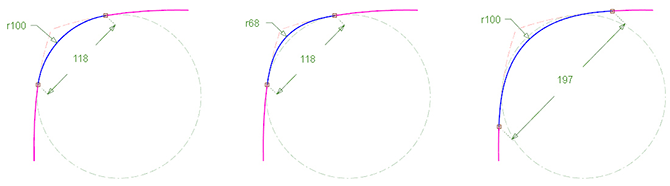
上图来自这,圆弧形成的圆角好处就是它的数字是确定的,也就是可以描述,可以口头传递,所以在设计和制作过程中,形态的传递很方便,比如说“R=5 mm”的圆角,即使我们在此处用 G2 的曲线来模拟,我们也会说 R 等于多少,自由曲线 NURBS 曲线是计算机来描述的,无法口头描述。所以在日常的工作中,我们通常会先确定这个 R 值,然后再来绘制过渡曲线,而我们绘制的 G2 曲线需要一个过渡的区间,这个区间往往需要比圆弧形成的圆角过渡更大,以便在中部达到跟圆弧圆角一样的数值,即我们确定的 R,如上图所示,左图为 G0 的圆弧圆角过渡,中间为变化区间不变,但是中间的 R 值就发生了变化,而右图则把两头的连接点位置向各自方向后退,以便曲线的中段达到所需的 R 值。
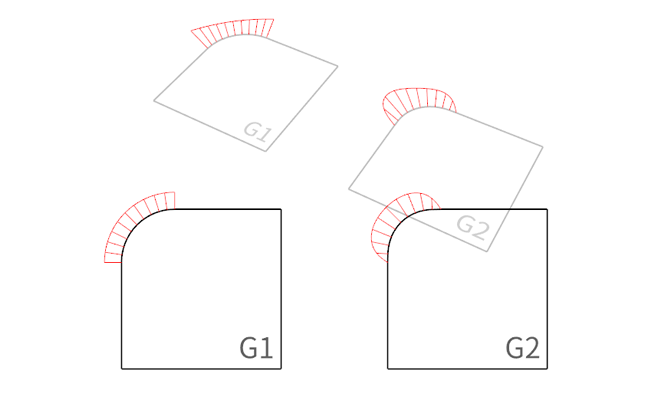
G1 和 G2 连续的不同数学特性不只是在正视的情况下能够识别出来,在透视的情况下也能分辨而出,透视是在视平面上的投射,所以是从 0 跳到一个数字,还是从 0 逐渐过渡到一个数字,投射之后这种特征是维持的。
但是最终作用于我们的是视觉效果,而不是数学关系,我们可以辨别处不同的顺畅程度,但是无法测出它的数学结构,而且我们看到的所有东西都是模拟世界的实体,数学只是对关系的一种归纳。就好像我们用放大镜去看产品的每条边线,它们都是连续的,只有我们通过辨别和归纳后,才能猜出设计师是否采用了 G2 曲线连续,所以,我们对曲线连续的分辨和执行,除了在软件中使用各种数学工具检测外,更重要的是退到宏观一层,就像去看待一个已经制造完的产品去观察。
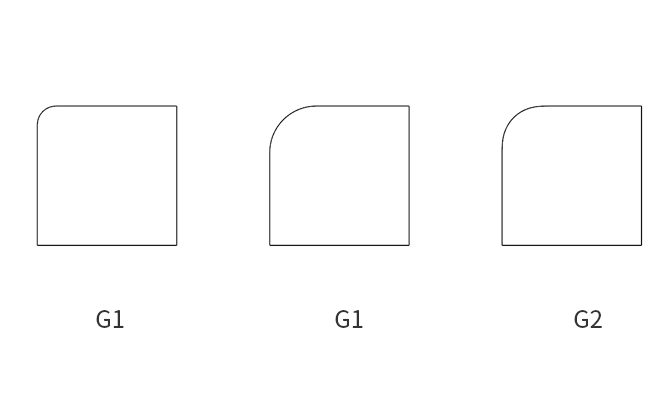
也就是说,并不是 G2 连续是万能的,或者时刻都必要的。
就好像《Privacy》这个视频中,我们最容易判断它是 G1 连续的就是来自与右上角的大圆弧,原因不在于它的 R 值大,而是与直线边形成的对比关系,比如上图所示的左图,就很难分辨出它是 G1 连续还是 G2 连续。
另外从制作的矢量图到输出成上图的点阵图,有一个栅格化的过程,栅格化就像是工业生产中的一种加工,它也有加工精度,加工会影响到最终曲线连续的视觉特征。比如在设计图纸上圆角过渡是 G1 切线连续,但是到了机床、抛光、打磨等等生产制程,圆角过渡可能变得更自然顺畅,尤其是如上图左这样的小圆角,如果是大圆角,像 JAL 商务舱旋转桌的左上角一样,就很难通过后续的加工过程来自我修正,因为它太大了必须在设计时就作出决定;在矢量图到点阵图的栅格化过程中也会如此,所以时刻关注宏观化后的效果也是同样重要的。
Last updated